Large Language Models are Surjective? Injective? Invertible?

Recently, there have been discussions on functional properties of Transformers, the basic building block of Large Language Models (LLM) and many other generative models. A paper ([1]) proves that Transformers can output anything given an appropriate input (surjective). After a few month, a followup ([2]) proves that LLMs always send different inputs to different outputs (injective), and hence we can invert the outputs back to inputs. These claims being said, wild thoughts about generative models start flowing around. Are jailbreaks fundamentally unavoidable? Are Transfomers lossless compression of knowledge? Do we have no privacy when we use LLMs? Does combining the two papers imply that LLMs are bijective? In this blog, we clarify the concepts of surjectivity, injectivity and invertibility that appear in these papers and explain their true implications.

What is Surjectivity/Injectivity/Invertibility?

These concepts are not hard to understand but the differences are nuanced. In the following, we will work with a function $f:\mathcal{X}\to\mathcal{Y}$.

• Surjective: Surjectivity means that for any $y$ from $\mathcal{Y}$, there exists an $x$ from $\mathcal{X}$, such that $f(x)=y$. In other words, every element in $\mathcal{Y}$ is reachable from some input from $\mathcal{X}$. A surjective function is also called an onto function.
• Injective: Injectivity means that for any two different $x_1,x_2$ from $\mathcal{X}$, the outputs $f(x_1),f(x_2)$ are also differnt. In other words, different elements from $\mathcal{X}$ are mapped to different elements in $\mathcal{Y}$. An injective function is also called a one-to-one function.
• Invertible: Invertibility means both surjectivity and injectivity. In other words, $f$ defines a correspondence between $\mathcal{X}$ and $\mathcal{Y}$, such that every elment in $\mathcal{X}$ correspond to a unique element in $\mathcal{Y}$ and vice versa. An invertible function is also called a bijective function. We can invert an output of an injective function uniquely to its input, but an injective function is not necessarily an invertible function.

Let us now look at some examples to understand their differences. We visualize three functions from two dimensional Euclidean space to itself, showing how the grids change according to the function.

(a) Surjective but not Injective The output covers the whole space, while self-crossing

(b) Injective but not Surjective Distinct inputs stay distinct, but an output region is not reached.

(c) Bijective Perfect one-to-one pairing.

OK cool! But what do they mean for generative models like LLMs?

Let us treat a generative model as a function $f$, where the input $x$ is the input we feed to the model, and output $y$ is the content the model generates. For now we do not specify what $\mathcal{X},\mathcal{Y}$ are exactly. Let us just think of them as input prompts and model responses for the moment and see what would happen if certain properties of $f$ were true.

When $f$ is surjective…

1. $f$ is surjective means that jailbreaks are unavoidable in principle because for any harmful output, there exists an corresponding input to the output, that jailbreaks the model.
2. The other direction is not correct. A generative model that can be jailbroken is not necessaily surjective. It can be the case that $f$ is not surjective but a harmful output falls in the range of $f$.
3. One may argue that an identity function $f(x)=x$ is surjective, but not harmful. In the LLM world, we can start the conversation with ‘Repeat the following sentences:’ to realize such function, given that the model is good at instruction following. One may further argue that the input corresponding to harmful outputs can be hard to find anyways. Indeed, surjectivity does not capture the capability of generative models, or how hard it is to find a corresponding input, and hence surjectivity alone does not imply that the model is unsafe in general. However, studying surjectivity is still a good starting point for safety. After all, we need to first ask whether jailbreaks are possible, and then ask whether jailbreaks are tractable.
4. When the generative model has physical consequences, surjectivity alone is already scary. A lot of robotics applications have started to use generative models due to their extraordinary capability. Let us say $\mathcal{X}$ is the visual inputs to a humanoid robot, and $\mathcal{Y}$ is the robot actions. A surjective policy $f$ would mean that there exists a video clip, such that when it is played to the robot, the robot goes to kill a person!

When $f$ is injective…

1. $f$ is injective means that it is possible to find out the input from the output in principle, and is hence vulnerable to privacy disclosure because no two inputs produce the same ouput.
2. Another interpretation of injectivity is that $f$ is a lossless compression of the input.
3. Just like surjectivity, Injectivity does not capture how hard it is to find a corresponding input. Hence injectivity alone does not guarantee that we could recover input from the output.

As stated above, both surjectivity and injectivity are mere existential properties. Proving that a function is surjective/injective does not necessarily provide us with an easy way of finding the corresponding inputs. However, the connection between these properties and real-world risks is not symmetric. A safety violation occurs when a harmful output can be produced — that is, when such an output lies in the model’s range. This connects directly to surjectivity: if the model is surjective onto the harmful set, then by definition, every harmful output can be generated. The existence itself already signals potential danger. A privacy violation, on the other hand, happens when private information can be recovered from the output, so whether we could find out the information is by definition important. Injectivity only says that each output corresponds to a unique input, but it does not tell us that this input can be feasibly reconstructed. The secret may remain safe even if the mapping is injective, as long as inversion is computationally or statistically hard. In short, surjectivity points to an immediate safety concern, whereas injectivity still depends on whether the inversion is actually achievable.

So, Are LLMs Surjective/Injective/Invertible?

Now let us look into the claims in [1] and [2] and see what can be said about Transformers. Transformers are sequence models, i.e. they input sequence of vectors $a_1,\dots,a_n$, and outputs sequence $b_1,\dots,b_n=\text{TF}(a_1,\dots,a_n)$. Here $a_1,\dots,a_n,b_1,\dots,b_n\in\mathbb{R}^d$ are all vectors of the same dimension. In language models, every element of the input token sequence $s_1,\dots,s_n\in\mathcal{V}$ come from a finite vocabulary set $\mathcal{V}$. We first turn discrete tokens into continuous embeddings via a function $a_i=\text{Embed}(s_i)$ before passing it to $\text{TF}$. Similarly, we also turn continuous embeddings to discrete tokens via another function $t_i=\text{Unembed}(b_i)$ before outputting.

Nowadays decoder-only Transformers like GPT decode iteratively in an autoregressive manner. We start from a prompt $s_1,\dots,s_n$. In each iteration we calculate $b_1,\dots,b_i=\text{TF}(a_1,\dots,a_i)$ from the already generated content $s_1,\dots,s_i$, decode the next token as $s_{i+1}=\text{Unembed}(b_i)$ and append it to the end of the existing content. The generation ends when we generate a special token $s_n=\texttt{EOS}$.

On Surjectivity of Neural Networks ([1])

This paper proves that $\text{TF}$ is a surjective function, no matter what the parameters are. However it does not prove that LLMs are surjective for the following two reasons:

1. This paper works in the continuous space, while the language models work in the discrete space.
2. This paper does not work with autoregressive generation.

This conclusion sounds reassuring for langauge models. However, the paper proves surjectivity results for broader popular generative model architecutres, such as diffusion models and robotics models. For these applications discretization and autoregressiveness do not exist, and hence the safety threats are more serious. One may refer to Section 4 of the paper for more discussions.

Language Models are Injective and Hence Invertible ([2])

This paper analyzes a different function from the last one. It proves that the function from $s_1,\dots,s_n$, the input token sequence, to $b_n$, the output embedding, is injective, excluding a negligible subset of $\text{TF}$’s parameter space. However, it does not prove that LLMs are injective from input sequences to output sequences, as different embeddings can lead to the same token.

Moreover, the function from input token sequence to output embedding is not surjective. This is because the set of input sequences is discrete and the set of output embeddings is continuous, and no continuous function with discrete inputs can be surjective on a continuous output. Hence this function is not invertible. The word invertible in the title is not used in a conventional way, and just mean that it is possible to invert an already generated output back to input.

Let us now comparing these two settings in a minimal setting. Let’s say the input is just a single token $s_1\in\mathcal{V}={\text{one},\text{day},\text{egg}}$, it is transformed into a 2-dimensional embedding $a_1$. The output $b_1=\text{TF}(a_1)$ is also two dimensional. According to [1] the function from $a_1$ to $b_1$ is surjective, and according to [2] the function from $s_1$ to $b_1$is injective. The $\text{TF}$ transformation looks like the following:

(a) Continuous to Continuous The output covers the whole space, while self-crossing.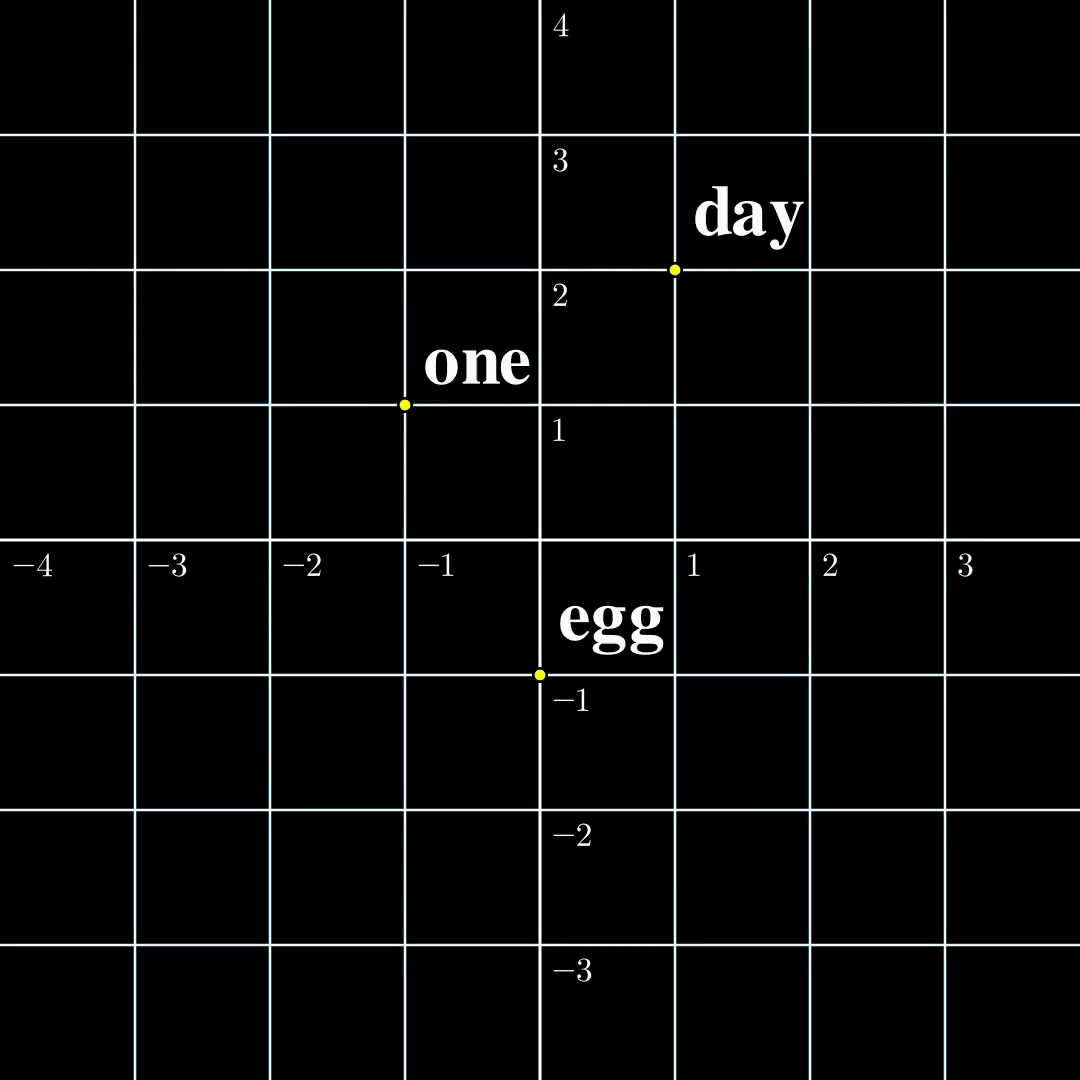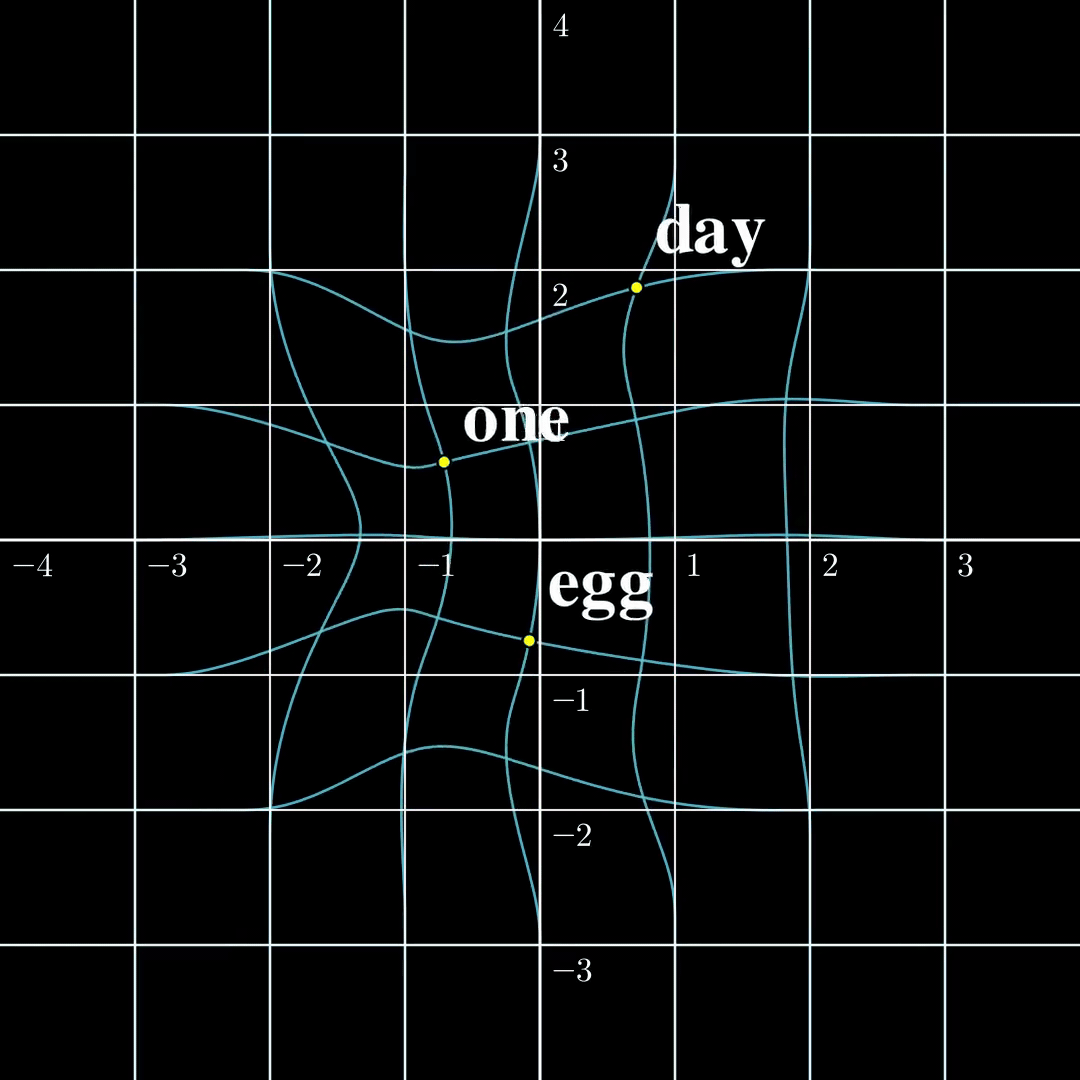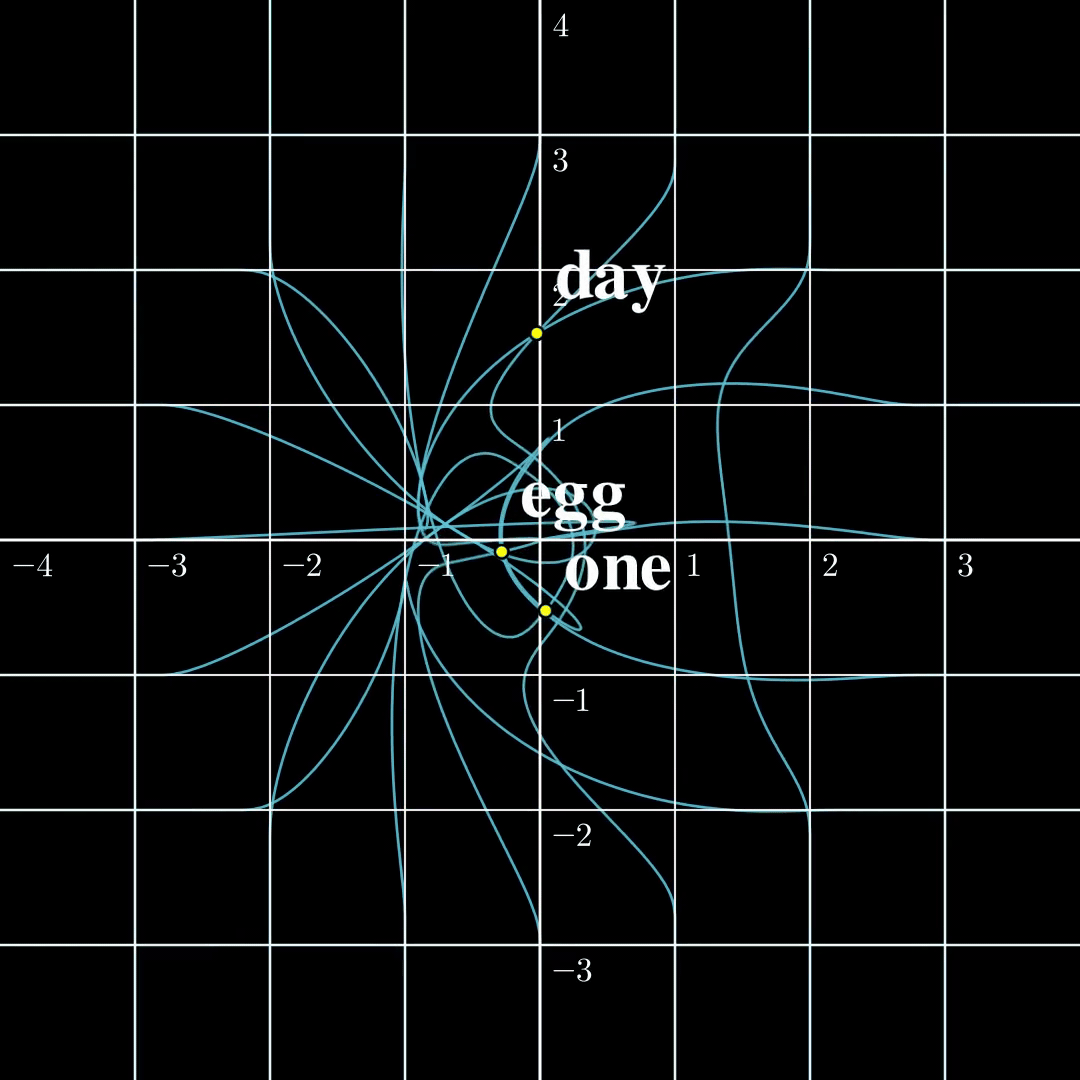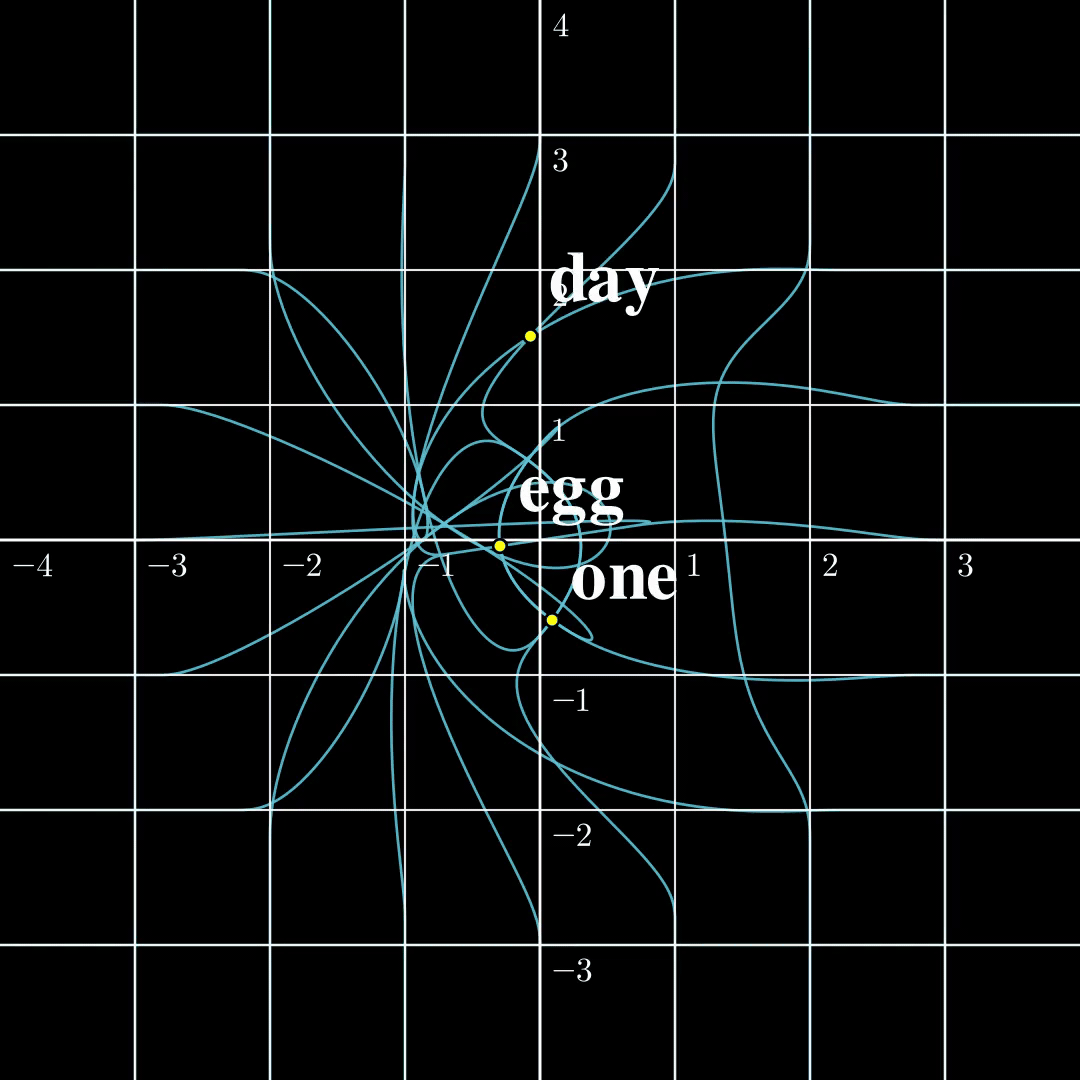

(b) Contrast The continuous function is surjective, while the discrete function is injective.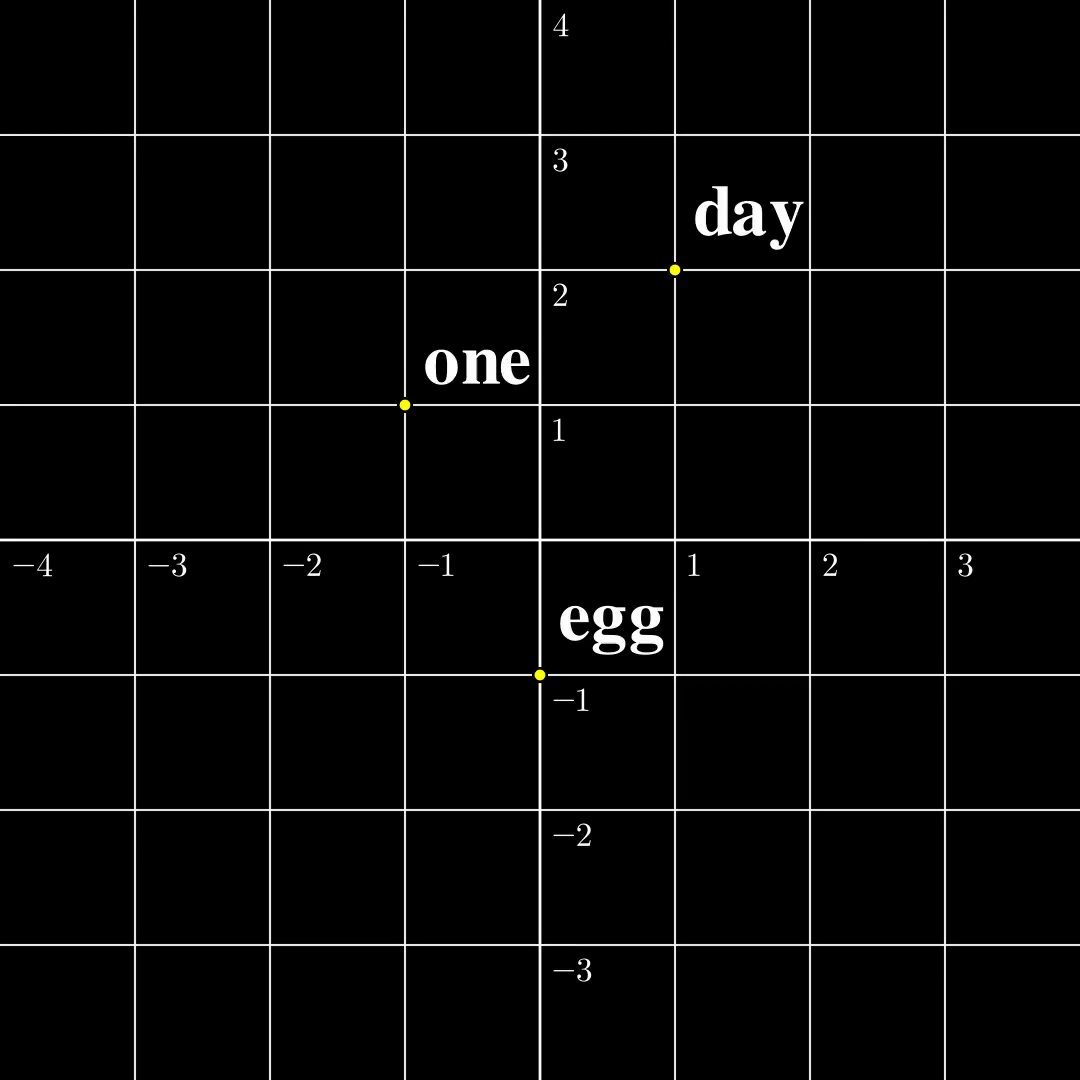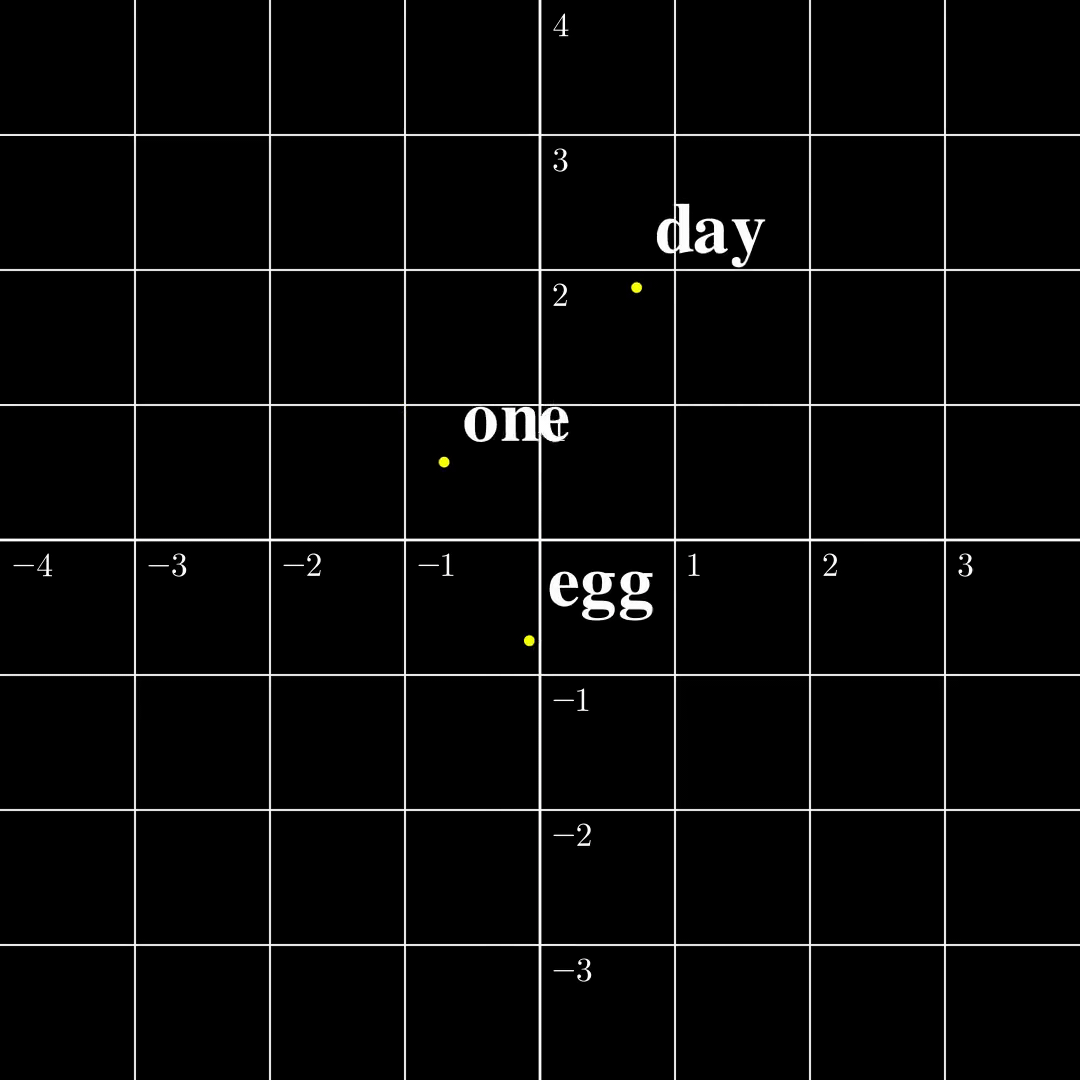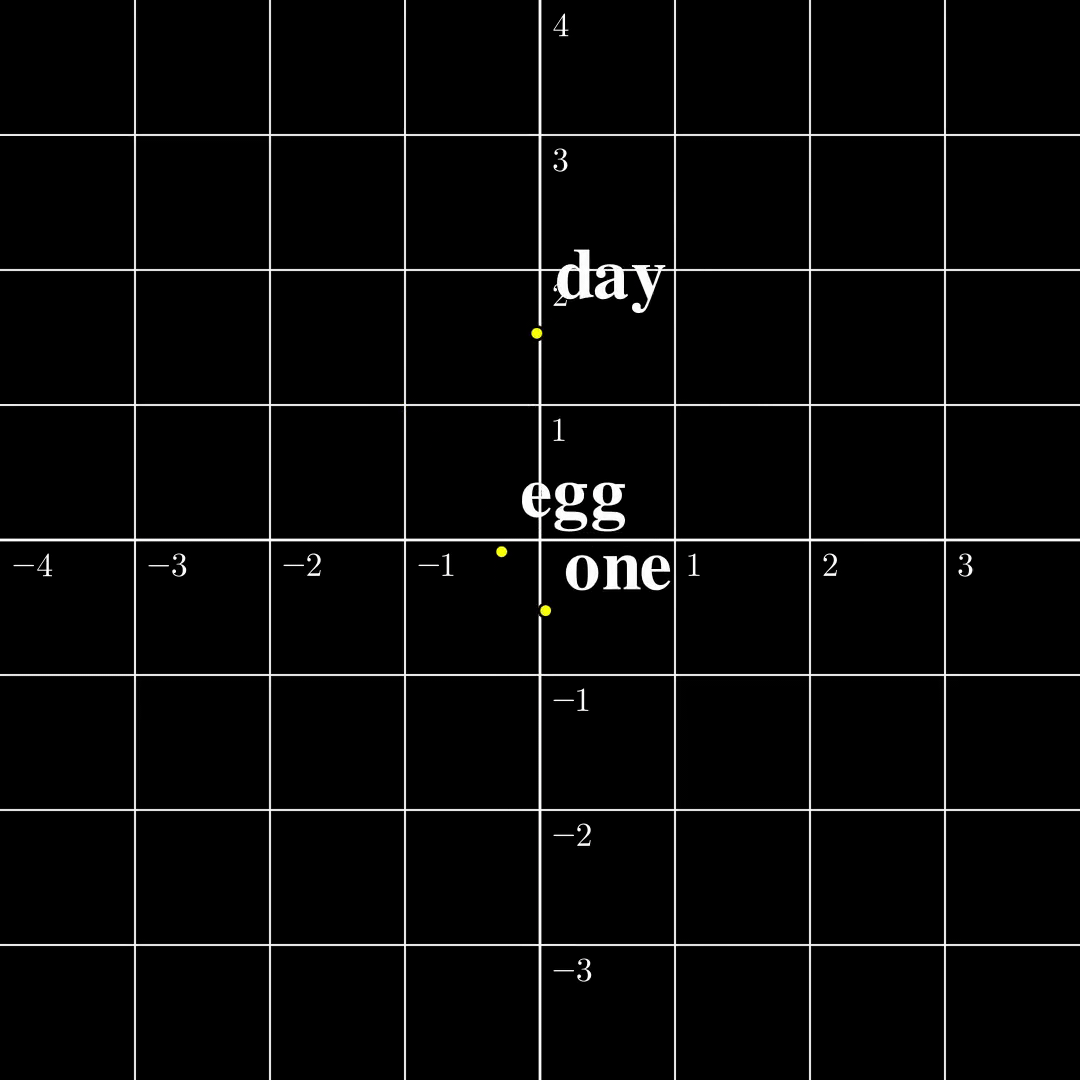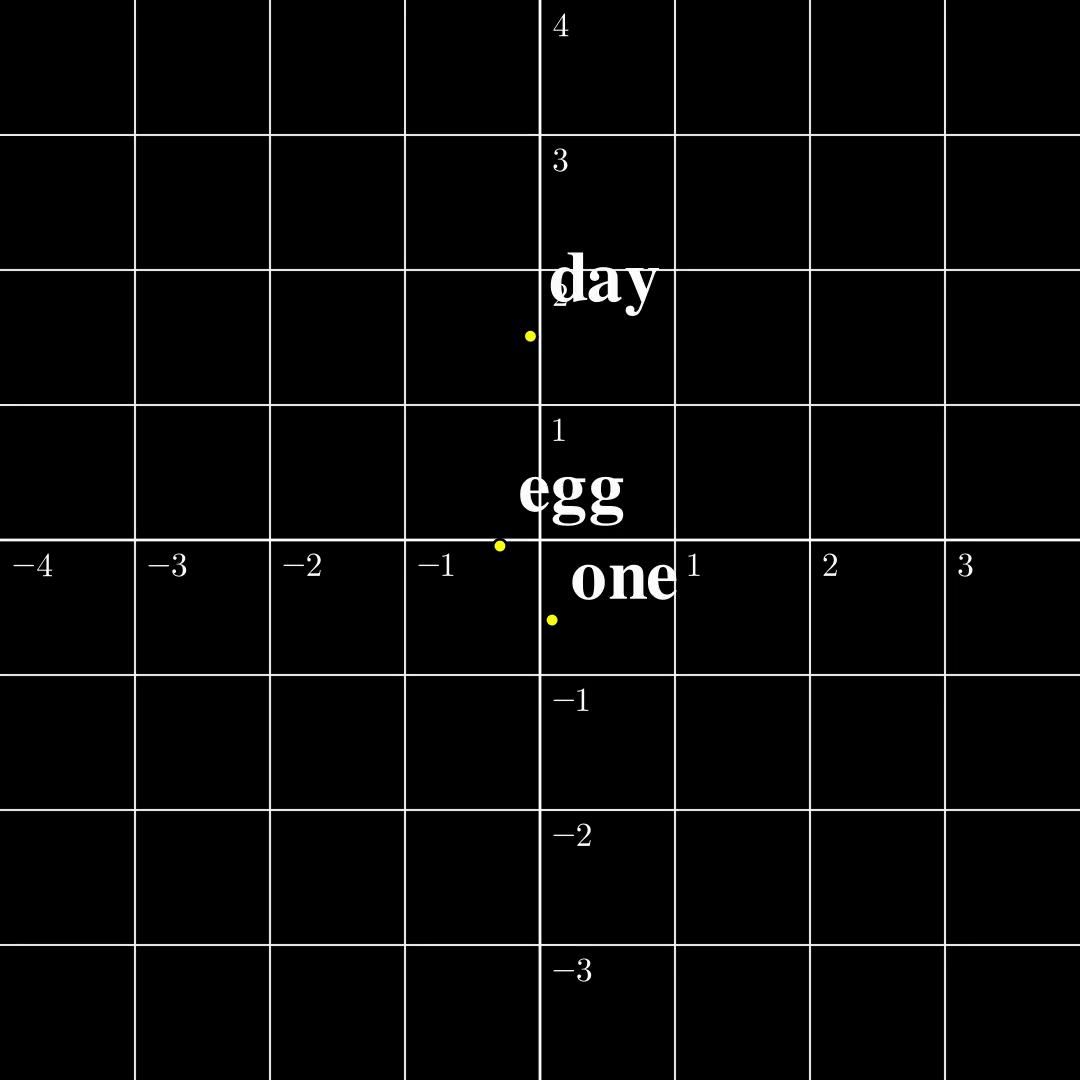

(c) Discrete to Continuous Different embeddings do not collide.

From this figure, the fact that a map from a discrete set to a continuous set is very likely injective should be intuitive. The rigorous proof is presented [1]. The surjectivity between two continuous spaces, however, is a lot trickier, and I will write another blog dedicated to explaining the intuitions and proofs. Furthermore, both papers provide similar algorithms to recover $a_1,\dots,a_n$ from $b_1,\dots,b_n$ given the parameters in $\text{TF}$, and the inputs turn out to be very easy to recover in this setting. However, this setting is far from useful and how to recover $s_1,\dots,s_n$ from $b_n$ remains elusive.

Concluding Remarks

After reading this blog, it should be clear that LLMs are neither surjective nor injective from input sequences to output sequences. Though surjectivity has safety implications and injectivity has privacy implications, these threats has not reached the realm of LLMs yet. The seemingly contradicting claims from the two papers stem from the fact that they are considering different functions. More broadly, surjectivity/injectivity could imply safety/privacy risks in domains where continuous inputs/outputs are present.

Reference

[1] Haozhe Jiang and Nika Haghtalab. On surjectivity of neural networks: Can you elicit any behavior from your model? arXiv preprint arXiv:2508.19445, 2025.

[2] Giorgos Nikolaou, Tommaso Mencattini, Donato Crisostomi, Andrea Santilli, Yannis Panagakis and Emanuele Rodolà. Language Models are Injective and Hence Invertible arXiv preprint arXiv:2510.15511, 2025.